Derivate – Ein Deep Dive in die Materie

Derivate verfügen, zusätzlich zu der Komplexität von herkömmlichen Aktien, über ihre eigenen Kennwerte, die sowohl vom Emittenten erhoben als auch von diesen eingeführt werden. Es kommt also auch hier wieder darauf an, wie der jeweilige Emittent diese Kennwerte berechnet und in welcher Höhe er sie auf das Derivat aufschlägt. 

Dieses Modell ist für uns als Anleger in Derivate besonders interessant, da es Aufschluss über die Preisbewertung von Derivaten gibt und Formeln für diese aufstellt. Um das Modell und die Preisbewerungsparameter zu verstehen, müssen wir einen etwas genaueren Blick darauf werfen:

Das Black-Scholes-Modell, auch bekannt als Black-Scholes-Merton-Modell, ist ein mathematisches Modell zur Bewertung von Optionen und anderen derivativen Finanzinstrumenten. Es wurde 1973 von Fischer Black, Myron Scholes und Robert Merton entwickelt und revolutionierte den Optionshandel, weil es eine geschlossene Formel zur Preisberechnung von Derivaten lieferte.

Die Mathematiker hinter dem Modell, Fischer Black, Myron Scholes und Robert Merton

Das Modell geht davon aus, dass der Preis des zugrunde liegenden Basiswerts (z. B. einer Aktie) einer geometrischen Brownschen Bewegung folgt und dass es möglich ist, ein risikoloses Portfolio durch Zusammenführen des Basiswerts mit der Option zu erstellen.

Die Brownsche Bewegung wurde ursprünglich vom Botaniker Robert Brown entdeckt, als er beobachtete, wie Pollenkörper im Wasser einer zufälligen - oder, um es mathematisch korrekt zu formulieren chaotischen - Bewegung folgen. Später wurde dieses Konzept von Physikern und Mathematikern, insbesondere Einstein und Wiener, formalisiert.

In der Finanzwelt wird die brownsche Bewegung nun genutzt, um die zufällige Natur von Aktienkursen mathematisch zu modellieren. Man geht davon aus, dass der logarithmierte Preis einer Aktie einer brownschen Bewegung mit Drift folgt, was als geometrische brownsche Bewegung bezeichnet wird. Mithilfe der Preisbewertungs-Parameter des Black-Scholes-Modell können wir Derivate basierend auf dieser Annahme also bezüglich ihrer Preisentwicklung bewerten. 

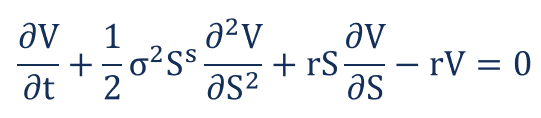
Diese Gleichung hinter dem Black-Scholes-Modell beschreibt den Preis von Aktienoptionen über die Zeit.

Diese Parameter, die wir uns im folgenen Abschnitt genauer anschauen wollen, variieren je nach Emittent (Anbieter) und Derivat, werden aber vor dem Erwerb des Derivats immer vom Emittenten angegeben. Nachdem wir uns diese genauer angeschaut haben, können wir die möglichen Risiken und Chancen eines Derivats also besser abschätzen.

In der Finanzwelt bezeichnet Volatilität die Kursschwankung eines Werts. Fällt und steigt eine Aktie bspw. regelmäßig um 20-30%, ist sie deutlich volatiler als eine Aktie, die im gleichen Zeitraum lediglich Kursschwankungen von 2-5% erfährt. Implizite Volatilität hingehen bezeichnet die erwartete, zukünftige Volatilität eines Werts. Sie gibt also Auskunft über die Erwartung der Anleger hinsichtlich der Schwankung dieses Werts.

Eine höhere implizite Volatilität bietet oft mehr Chancen für Preisbewegungen, was das Derivat attraktiver - aber auch gefährlicher - macht. Da Anleger bei Brokern, die keine Margin Calls erlauben, jedoch nur 100% ihres Investments verlieren und insbesondere bei Derivaten ein Vielfaches davon gewinnen können sorgt eine hohe, implizite Volatilität oft für einen höheren Preisaufschlag seitens des Emittenten auf das Derivat, das auf diesen Wert aufbaut.

Die sogenannten Griechen sind Kennzahlen, die die Sensitivität des Derivatsspreises gegenüber verschiedenen Einflussfaktoren messen. 

Das Delta gibt an, um welches Vielfache sich der Preis eines Derivats verändert, wenn der Preis des Basiswerts - also in unserem Fall der zugrunde liegenden Aktie - bewegt. Um das besser zu verstehen, sollten wir erneut ein Beispiel betrachten.

Eine Aktie der Firma Microsoft kostet 100 Euro. Du benötigst also 100 Euro, um eine einzige Aktie zu kaufen. Ein bestimmtes Derivat, das die Microsoft-Aktie als Basiswert verwendet, kostet 10 Euro. Dieses Derivat verfügt über ein Delta von 0.5. Das bedeutet nun, das der Preis des Derivats sich für jede Preisveränderung des Basiswerts um das 0.5-fache dieser Preisveränderung bewegt. Steigt die Microsoft-Aktie also um 1 Euro, steigt unser Derivat im Wert um 0.50 Euro. 

Moment mal. Das klingt ja, als würden wir nur die Hälfte des Gewinns einfahren, den wir mit dem Basiswert verdienen könnten. Ist das Derivat also viel schlechter als die Aktie? Nein! Wenn die Aktie um 1 Euro steigt, fährt sie, aufgrund dessen, das sie zuvor bei 100 Euro stand, 1% Gewinn ein. Unser Derivat steigt dadurch um 1 Euro * 0.5 = 50 Cent, stand allerdings zuvor bei nur 10 Euro, gewinnt dadurch also um 5% an Wert!

Da wir von den selben 100 Euro, die wir für eine Aktie zahlen würden, 10 Derivate kaufen können, bedeutet das für uns, das ein Delta von 0.5 einen Hebel von 5 für unser Investment darstellt.

Tatsächlich ist dies auch die Methode, mit der der Hebel, der zu dem jeweiligen Derivat angegeben wird, berechnet wird. Wir multiplizieren hier das Delta mit dem Aktienkurs und teilen es durch den Optionspreis. In unserem Beispiel also:

0.5 * 100 / 10 = 5

Und schon errechnen wir unseren vorher numerisch identifizierten Hebel von 5. Da der Hebel bei Derivaten bereits oft mit angegeben wird, können wir uns diese Berechnung zwar sparen, dennoch ist es nicht unerheblich, das Delta unseres Derivats zu kennen, um zu wissen, wie die Bepreisung zustande kommt.

Gamma gibt die absolute Veränderung des Deltas bei Bewegung des Preises des Basiswerts an. Wenn die Aktie sich also vergünstigt oder verteuert, sinkt oder steigt das Delta. Diese Veränderung des Deltas bezeichnet man als Gamma. Hohe Gamma-Werte bedeuten in diesem Zusammenhang, dass sich das Delta - und damit auch der zugrunde liegende Hebel - schnell verändert.

Im Allgemeinen bedeutet ein hoher Gamma-Wert also potenziell mehr unerwartete Volatilität durch die Änderung des Hebels, sodass die voraussichtliche Rendite - wenn auch immer berechenbar - schnell durch diese zusätzliche Komplexität an Greifbarkeit verliert.

Auch hier können wir wieder unser Beispiel von zuvor betrachten: Ein Derivat auf die Amazon-Aktie bei 100 Euro zum Derivatspreis von 10 Euro verfügt über ein Delta von 0.5 (und damit einen Hebel von 5) sowie ein Gamma von 0.1. Die 0.1 geben die absolute Veränderung des Deltas bei Veränderung des Preises um eine Einheit an. Eine Einheit ist in den meisten Fällen 1 Euro oder 1 $. Steigt also die Microsoft-Aktie um 1 Euro auf 101 Euro, so steigt das Delta auf 0.5 + 0.1 = 0.6. Das ergibt, multipliziert mit dem gestiegenen Kurs des Basiswerts und geteilt durch den erhöhten Derivatspreis einen neuen Hebel von ~5,78.

Das Gamma gibt also an, wie aggressiv sich dein Delta und damit auch dein Hebel durch Volatilität - also Kursschwankungen - verändert. Ein niedrigeres Gamma ist für vorsichtige Investoren also deutlich attraktiver, um eine stabilere Preisbildung erwarten zu können.

Um zu verstehen, welche Rolle Vega in der Preisberechnung von Derivaten spielt, müssen wir uns die implizite Volatilität, die wir weiter oben betrachtet haben, erneut ins Gedächtnis rufen. Vega misst nämlich die absolute Preisveränderung des Derivats, wenn die implizite Volatilität (IV) um 1 Prozentpunkt steigt. Hohe Vega-Werte bedeuten also, dass der Preis unseres Derivats stark auf die Änderung der IV reagiert.

Betrachten wir nun erneut das Beispiel, anhand dessen wir bereits die vorherigen Griechen erklärt haben. Unser Derivat kostet 10 Euro und das Vega liegt bei 0,2. Steigt die IV also um 1%, erhöht sich der Preis/Wert unseres Derivats um 0.2 Einheiten, im Falle von Euro also auf 10,20 Euro. Sinkt die IV stattdessen um 2%, fällt auch der Preis/Wert unseres Derivats um 0.2 * 2 = 0.4 Einheiten, 40 Cent, also auf 9,60 Euro.

Eine hohe Erwartung an die Schwankungsbreite des Werts einer Aktie hat also bei existierendem Vega zur Folge, dass der Preis des darauf basierenden Derivats höher ist, dessen Wert aber auch gleichzeitig steigt. Für den Emittenten ist das förderlich: Der erhöhte Preis steigert den Gewinn am angebotenen Derivat und die Erwartung höherer Schwankungen und somit Renditen lockt zusätzliche Käufer an. 

Wenngleich dies für den Käufer ebenso förderlich ist, ist es wichtig, sich vor Augen zu führen, dass diese verbesserte Chance auf Profit keine Almosen seitens des Emittenten darstellen. Das Wertpapier könnte tendenziell stärkeren Schwankungen unterliegen, die auch ins Minus laufen können.

Das Theta misst den absoluten Wertverfall eines Derivats pro Tag. Derivate verlieren also an Wert, während ihre Restlaufzeit sich verkürzt. Dieses Theta ist in jedem Fall negativ, da Derivate durch Verkürzung der restlichen Laufzeit an Wert verlieren und nie - zumindest nicht durch diesen Parameter - gewinnen. Zur Berechnung des neuen Preises unseres Derivats nach Ablauf eines Tages addieren wir das Theta einfach auf den aktuellen Preis unseres Derivats.

Gehen wir davon aus, unser Derivat für 10 Euro hat einen Theta-Wert von -0.10. Dieser Wert ist tendenziell recht hoch angesiedelt, erfüllt aber seinen Zweck zur Vereinfachung unseres Beispiels: Nach einem Tag ist das Derivat nun nur noch 10 + (-0.10) = 9,90 Euro wert.

Aufgrund dieser Theta-Mechanik ist es ratsam, Derivate vor Ablauf ihrer Restlaufzeit zu verkaufen und diesen nicht auszureizen, wenn man bis dahin keine überproportionalen, weiteren Gewinne erwartet.

Wie wir in diesem Artikel herausgefunden haben, kann die Preisberechnung eines Derivats sehr komplex sein, insbesondere aufgrund der Verwogenheit der einzelnen Parameter miteinander. Dazu kommt, das viele dieser Parameter Absicherungen seitens des Emittenten darstellen, um den möglichen Gewinn des Anlegers möglichst weiter klein zu halten.

Werte wie das Theta sollen den Anleger dazu verleiten, schnelle Gewinne zu jagen, da längerfristig gehaltene Positionen abgestraft werden. Preisprognosen für Aktien lassen sich im Allgemeinen schon schwer treffen, doch werden diese unter schrumpfendem Beobachtungszeitraum nur noch deutlich ungenauer. Werte wie das Gamma führen dazu, das ein Verkaufsschock einer Aktie schnell einen Totalverlust im Derivat zur Folge hat. Werte wie das Vega wiederum sollen Kunden dazu verlocken, teurere Derivate zu kaufen und locken mit erhöhtem Gewinn- sowie aber auch Verlustpotenzial.

Ich möchte darauf hinaus, das all diese Faktoren nicht von irgendwo kommen und hier ein - vermeintlich - kugelsicheres System konstruiert wurde, um mit profitgierigen Anlegern Kasse zu machen. Und genau das ist schließlich die Realität: Der Emittent, meist eine Bank, würde das Derivat nicht freiwillig anbieten, wenn er damit im Durchschnitt keinen Gewinn erzielen könnte. Im Gegensatz zu Aktien, bei denen wir uns produktiv durch die Investition am Wachstumspotenzial eines Unternehmens beteiligen, spielen wir bei Derivaten gegen den Emittenten. Entweder er gewinnt oder wir tun es. Das erinnert an das aus der Glücksspiel-Szene bekannte Sprichwort 'Die Bank gewinnt immer', was schlicht daran liegt, dass Derivate im weitesten Sinne genau das sind: Glücksspiel. Es wird immer eine handvoll Anleger geben, die ihr Investment aus schierem Glück durch ein Derivat vervielfacht haben, doch gibt es für jeden Anleger, der sein Kapital verzehnfacht mindestens 10 Anleger, die ihr gleichwertiges Kapital gänzlich verloren haben.

Ich möchte nicht ausschließen, das es mit einem sehr ausgeklügelten System immer noch möglich ist, systematisch Gewinn mit Derivaten zu generieren. Es sei jedoch gesagt, das Derivate jenseits solcher hochspezialisierten Systeme hochriskant sind und tendenziell eher zum Verlust als zum Gewinn führen.